Pre-processor Software for Calibration of LS-DYNA® Material Models
Hubert Lobo
Matereality - New York, USA
Abstract
LS-DYNA contains a wealth of material models that allow for the simulation of transient phenomena. These models are often quite complex and difficult to calibrate. We present CAE Modeler, a generalized pre-processor software used to convert material property data into material parameters for different material models used in CAE. In this paper, CAE Modeler is used to streamline the conversion of rate dependent stress-strain data into material parameters for the MAT_024 material model. The interactive software is capable of handling all three rate dependency options of MAT_024 and outputs a data file that can be read directly into LS-DYNA. Support for other material models is envisaged.
Introduction
Over 200 material models are available today for the benefit of the LS-DYNA user. These are designed to capture a variety of phenomena on an incredible variety of materials ranging from metals and composites to foams, rubber and even human tissues. It is natural that the material models needed for such diverse materials contain some level of complexity. Different kinds of tests are needed which need to be conducted in a variety of modes and test conditions. The data then needs to be transformed and pieced together in a particular manner to provide a coherent and self-consistent description of the desired material behaviour to the simulation. This is not an easy task, commanding the skills of a material scientist, mechanical engineer and simulation expert. While extensive documentation is provided in support of each material model, a single misunderstanding of the intent of the material model developer can result in a defective material model being used in the simulation. Unfortunately, with the number of options and settings that accompany each material model, this can happen quite easily and great care must therefore be exerted by the CAE analyst in order to ensure a good simulation. All this takes time and effort and detracts from the true task of the CAE analyst which is to analyse the outcome of the simulation which is itself a formidable task.
In this paper, we present a cloud-based software that attempts to address the issues related to the set-up and calibration of material models for LS-DYNA. We take aim at MAT_PIECEWISE_LINEAR _PLASTICITY (MAT_024), perhaps the most commonly used material model to see if we can develop a solid methodology for the conversion of rate-dependent stress-strain curves into a MAT_024 material card. Realising that all three rate dependency options are in common use, the software allows the user to select for and then transform the data as desired. A semi-automated conversion process is used whereby the user can interact with the software to further tune and modify the material model parameters to his or her needs. The outcome is a data file that can import the material card directly into the LS-DYNA software.
It is anticipated that this software can then be extended to provide the same conversion capability for other commonly used LS-DYNA material models.
The MAT_024 Material Model
The MAT_024 material model is commonly used to model a variety of materials in LS-DYNA. While created originally for metals it is often used for plastics with certain known limitations, which have been described in previous work [1]. MAT_024 is a rate-dependent elastic-plastic material model [2]. The basis of the model therefore is an elastic-plastic formulation where the quasi-static stress-strain curve is decomposed into a linear elastic component followed by a non-linear plasticity curve which accounts for the post-yield inelastic deformation of the material. Only the plasticity data are rate-dependent. In the case of metals, this decomposition is usually unambiguous but with plastics, some guesswork or estimation is needed to arrive at a suitable compromise on account of the fact that plasticity commences prior to yield (Figure 1). This conversion process is sometimes not properly implemented with a number of possible errors coming into play, e.g., the use of engineering instead of true stress-strain data or the substitution of true-strain for plastic strain.
There are three options for handling rate dependency. The most commonly used is the CP option where a Cowper-Symonds equation is fitted to yield stress v. strain rate data. The resulting two equation coefficients are entered into the model, allowing the simulation to scale the quasi-static plasticity curve to higher strain rates. The second option permits the direct input of a table of normalized yield stress v. strain rate data (LCSR) as a means to represent the rate dependency. The resulting interpolated scale factor is then used to scale the quasi-static plasticity curve. In the third option, the plasticity data for each stress-strain curve is input independently as a family of curves (LCSS).
The decision about which option to use rests clearly with the user; however it is somewhat common practice to use the Cowper-Symonds option for metals because this equation does a good job of representing the rate dependency of these materials. It provides smooth scaling and can extrapolate in strain-rate. In contrast, the rate dependency of most plastics is linear with the logarithm of strain rate. This does not model well with Cowper-Symonds suggesting the use of one of the other two options for these materials. The LCSR table is commonly used for plastics. The actual data can be linearized with an Eyring equation if needed in order to smooth the scaling. The LCSS option has adherents who wish to precisely model each stress-strain curve. It is particularly valuable where the plasticity curves change shape with strain rate, where significant model infidelity would be introduced by the simple scaling of the quasi-static curve. However, the LCSS option is difficult to implement correctly on account of two factors. It is a preference for many analysts that each of the true stress-plastic strain data pairs be taken at the same plastic strain for each strain rate; this is not easily calculated. Second, should the stress-strain curves change shape, there is a risk of crossover, negative slopes and non-existence of corresponding plasticity strains at higher strain rates. Artificial constructions are then needed to overcome these problems such as the addition of fictive data points to maintain correct trends suitable for simulation. Each of these factors introduces error to the material model.
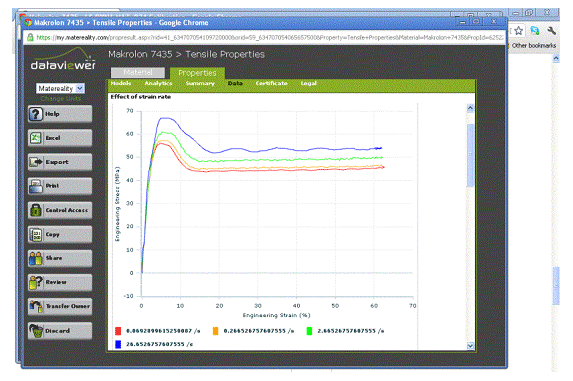
Figure 1: Typical rate-dependent tensile data for a plastic
In the classic case where the material data are well behaved where each stress-strain curve has the same curve shape but is simply shifted upward with increasing strain rate as seen for example in Figure 1, there is no particular benefit in using the LCSS option over the LCSR since each will model the data with equal fidelity.
Finally, post-yield behavior in MAT_024 assumes that the failure strain is rate independent so that the material fails at the same strain no matter what the strain rate. This is true for metals but often not the case for plastics.
CAE Modeler
CAE Modeler is a generalized materials pre-processor software created to take material property data and convert it to material model inputs for various CAE applications. The cloud based software (SAAS) operates on material properties stored in databases on the Matereality cloud. The databases can contain a variety of properties of materials not all of which are suitable for explicit simulation. Because each material model has specific data requirements, the software first assembles materials that have the required properties from the material database (Figure 2). For example, in the case of MAT_024 models, it will select only rate-dependent material data. Additional density and Poisson�s ratio values are sourced if available.
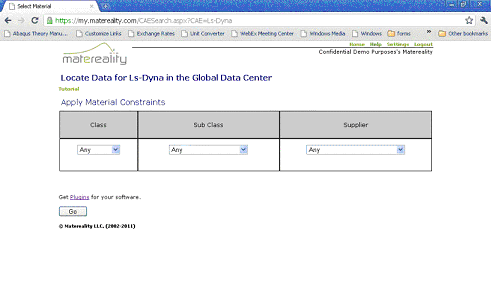
Figure 2: A search engine used to assemble required properties
The software then presents a list of materials for which a MAT_024 model can be created. (Figure 3). With this raw data, the CAE Modeler software commences a data transformation process to convert the stress strain data into the required parameters of the MAT_024 model (Figure 4). Consistent unit systems are applied, an important step, because units in LS-DYNA can be somewhat esoteric and consequently a source of conversion error (Table 1). If data is in engineering form, it is converted to true stress-strain. The transformation continues with the analysis of the quasi-static curve where the modulus is computed and the subsequent points for the plasticity curve are selected using a smart algorithm. Because of the extreme variety of possible post-yield behaviors, the automated calculation stops if a point of negative slope is observed. The selected plasticity points are visually presented to the user on an interactive plot of the stress-strain curves. The user can then manipulate the material parameters to arrive at the best model. For example, the model can be stiffened by increasing the modulus. This will shift the initial modulus line and recalculate the plasticity data. Plasticity points can be added or removed by clicking on the plot. This is particularly useful to add post-yield behaviors according to rules familiar to the particular analyst. A zoom feature is also useful to check the first plasticity point to ensure that it does not have any inflections where it meets with the modulus line.
Table 1: Example of LS-DYNA unit systems and its effect on property units
| Unit/Property |
A |
B |
C |
| Length |
m |
mm |
mm |
| Time |
s |
s |
ms |
| Mass |
kg |
tonne |
kg |
| Force |
N |
N |
KN |
| Modulus |
Pa |
MPa |
GPa |
| Stress |
Pa |
MPa |
GPa |
| Density |
kg/m3 |
tonne/mm3 |
kg/mm3 |

Figure 3: List of MAT_024 compatible materials; selecting a material starts the conversion process
At this stage the rate dependency can now be modelled. The CAE Modeler computes and presents the normalized yield stress v. strain rate. Should the Cowper-Symonds option be selected, (Figure 5) this data is fit to the Cowper-Symonds equation and the C and P values are filled in. The CAE Modeler then calculates and displays the resulting model points against the stress-strain data allowing the user to assess the effectiveness of the rate dependency modelling. The user has the ability to modify C and P to improve the model if desired and the effect of these changes are immediately reflected in the plot.
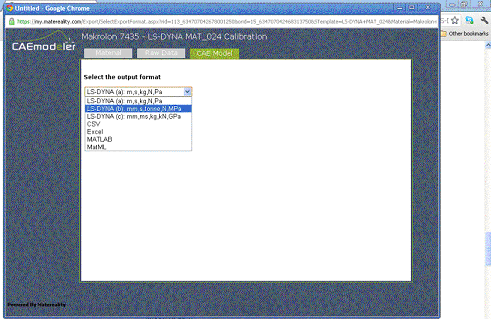
Figure 4: Selecting LS-DYNA unit systems prior to parameter conversion
In this way, the model can be rapidly improved as desired. Selecting the LCSS option permits the scaling of the quasi-static curve based on stress ratios. These values can be changed and the effect immediately observed in the display.
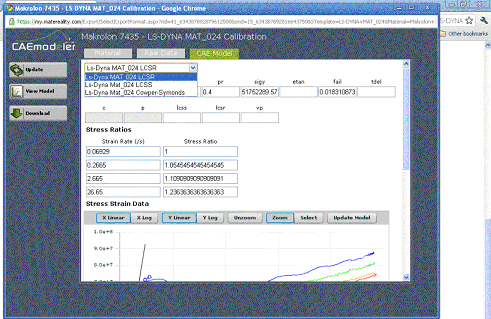
Figure 5: Selecting rate dependency modeling options
Finally, for the LCSS option model points can be picked directly off the plot permitting a rapid conversion of the stress-strain data into plasticity points.
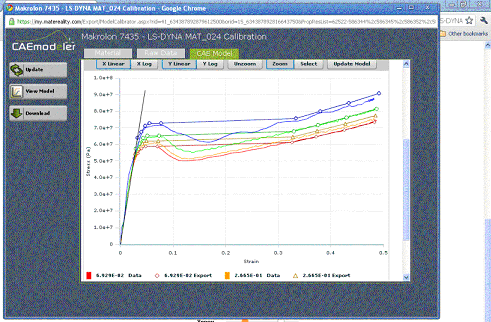
Figure 6: Finalized material model viewed against raw tensile test data
In this way, a finalized material model is quickly obtained with a minimization of conversion error (Figure 6). The material card can now be downloaded to the user�s desktop as a file that can be imported directly into LS-DYNA.
Conclusions and Future Work
A software has been created that streamlines the process of converting rate dependent stress-strain data into a MAT_024 material model. The conversion process automates a number of processes including transformation of engineering to true stress-strain and the use of self-consistent LS-DYNA unit system. The conversion of stress strain data to elasto-plasticity is facilitated by a graphical user interface which displays the model points in the familiar context of the original stress-strain data. Highly interactive capabilities permit rapid tuning to change modulus, selection of additional plasticity points or different rate dependency options. Data fitting software is employed where certain model components are represented by equations such as Cowper-Symonds. The resulting material model reads directly into LS-DYNA. In this way, the user is liberated from the technicalities of the model parameter creation process and can focus completely on building robust and well-tuned material models based on skill and intuition. The rapid conversion process allows for different options to be tried out increasing the efficiency and accuracy of the simulation process.
It is anticipated that the CAE Modeler software will be expanded to accommodate other commonly used material models such as MAT_STRAIN_RATE-DEPENDENT_PLASTICITY (MAT_019) and MAT_PLASTICITY_POLYMER (MAT_089) and MAT_SAMP-1 (MAT_187). Rubber material models will be facilitated by the addition of hyperelastic equation data fitting such as Mooney-Rivlin or Ogden equations. Foam models such as MAT_FU_CHANG (MAT_83) and MAT_CRUSHABLE_FOAM (MAT_63). The software and database are of such capability that there is no limit to they kind of material property that can be stored or the transformations needed to prepare it for LS-DYNA. In this way, a generalized material modelling pre-processor will be available for LS-DYNA.
References
[1] Lobo, H. Croop, B, �NAFEMS World Congress Proceedings� (2009)
[2] LS-Dyna Theory Manual, (2007)
[3] LS-Dyna Version 971 Keyword User�s Manual, (2007)
Phone: 607 257 1784 Fax: 607 266 0168
Email: info@matereality.com
|